字节流练习:图片复制
本文共 1311 字,大约阅读时间需要 4 分钟。
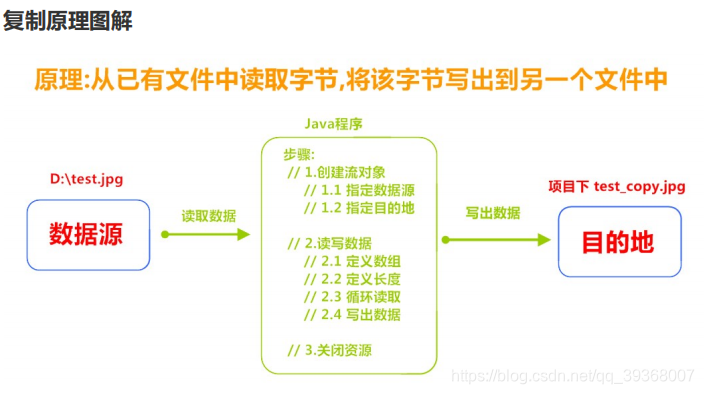

文件复制练习:一读一写
明确:
数据源: c:\\1.jpg 数据的目的地: d:\\1.jpg文件复制的步骤:
1.创建一个字节输入流对象,构造方法中绑定要读取的数据源 2.创建一个字节输出流对象,构造方法中绑定要写入的目的地 3.使用字节输入流对象中的方法read读取文件 4.使用字节输出流中的方法write,把读取到的字节写入到目的地的文件中 5.释放资源package com.itheima.demo03.CopyFile;import java.io.FileInputStream;import java.io.FileOutputStream;import java.io.IOException;public class Demo01CopyFile { public static void main(String[] args) throws IOException { long s = System.currentTimeMillis(); //1.创建一个字节输入流对象,构造方法中绑定要读取的数据源 FileInputStream fis = new FileInputStream("c:\\1.jpg"); //2.创建一个字节输出流对象,构造方法中绑定要写入的目的地 FileOutputStream fos = new FileOutputStream("d:\\1.jpg"); //一次读取一个字节写入一个字节的方式 //3.使用字节输入流对象中的方法read读取文件 /*int len = 0; while((len = fis.read())!=-1){ //4.使用字节输出流中的方法write,把读取到的字节写入到目的地的文件中 fos.write(len); }*/ //使用数组缓冲读取多个字节,写入多个字节 byte[] bytes = new byte[1024]; //3.使用字节输入流对象中的方法read读取文件 int len = 0;//每次读取的有效字节个数 while((len = fis.read(bytes))!= -1){ //4.使用字节输出流中的方法write,把读取到的字节写入到目的地的文件中 fos.write(bytes,0,len); } //5.释放资源(先关写的,后关闭读的;如果写完了,肯定读取完毕了) fos.close(); fis.close(); long e = System.currentTimeMillis(); System.out.println("复制文件共耗时:"+(e-s)+"毫秒"); }}
转载地址:http://rtwnz.baihongyu.com/
你可能感兴趣的文章